大厂笔试真题
20 多家大厂,100 道笔试真题,附带判题系统 和 题解。
对于准备春招和校招的录友,笔试很重要,练习笔试的最好方式,就是做历年题,大厂们重复出题的概率还是挺高的。
截止今天(2025 年 2 月 21 日)卡码网周赛已经举办了49期,关于大厂笔试的就有33场,昨天周赛(小红书24年春季笔试笔试)刚刚结束。
目前卡码网包含了 20 多家大厂笔试算法真题。
我们不仅给大家制作题目、输入数据和后台判题数据,还给大家写了每道题目的题解,工作量非常大。
所以再三考虑后,为了卡码网周赛可以长期稳定的举办下去,卡码网的笔试真题开始作为收费项。
我们的题库包含:20 多家大厂,100 道笔试真题,附带判题系统 和 题解。
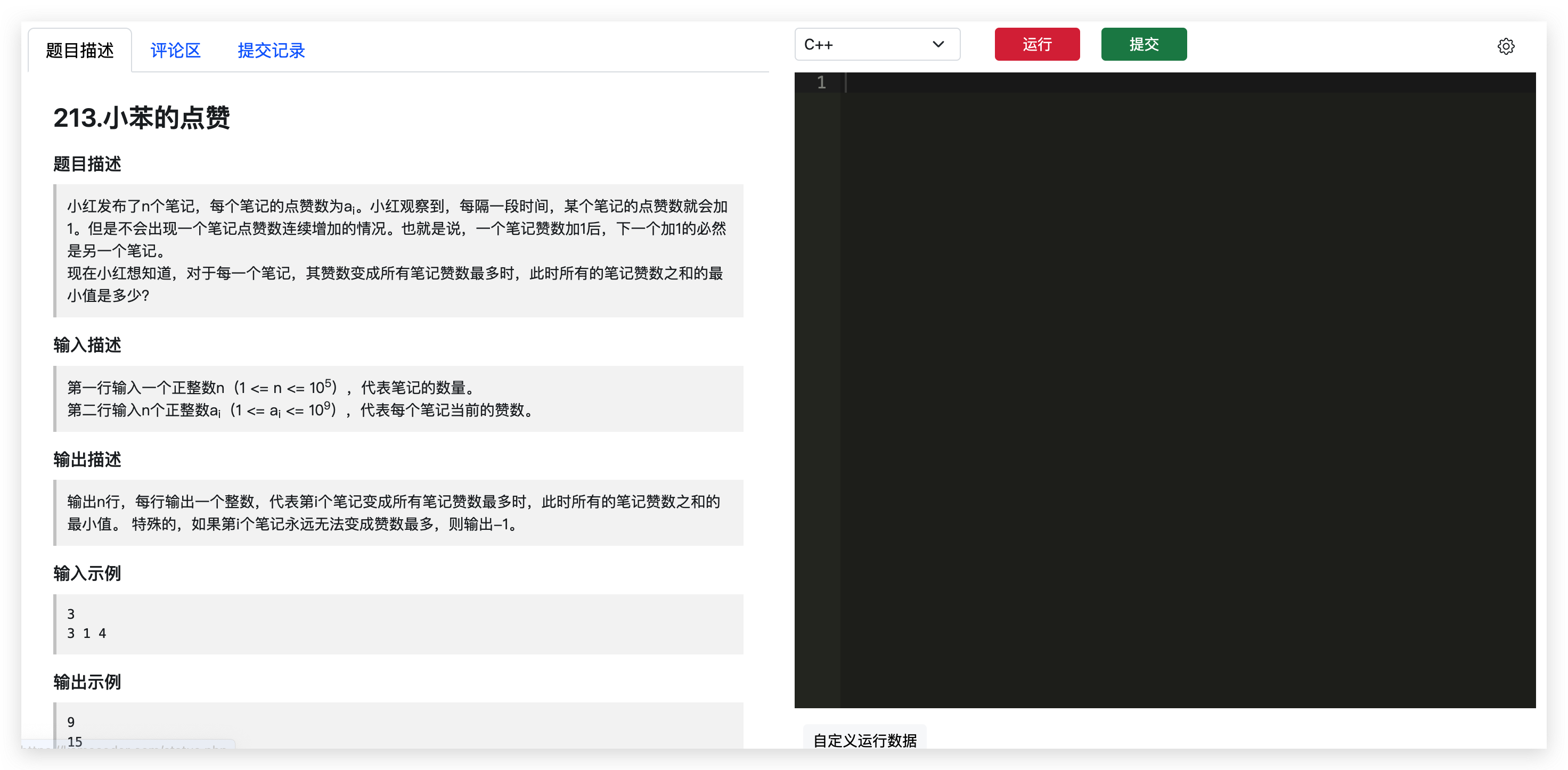
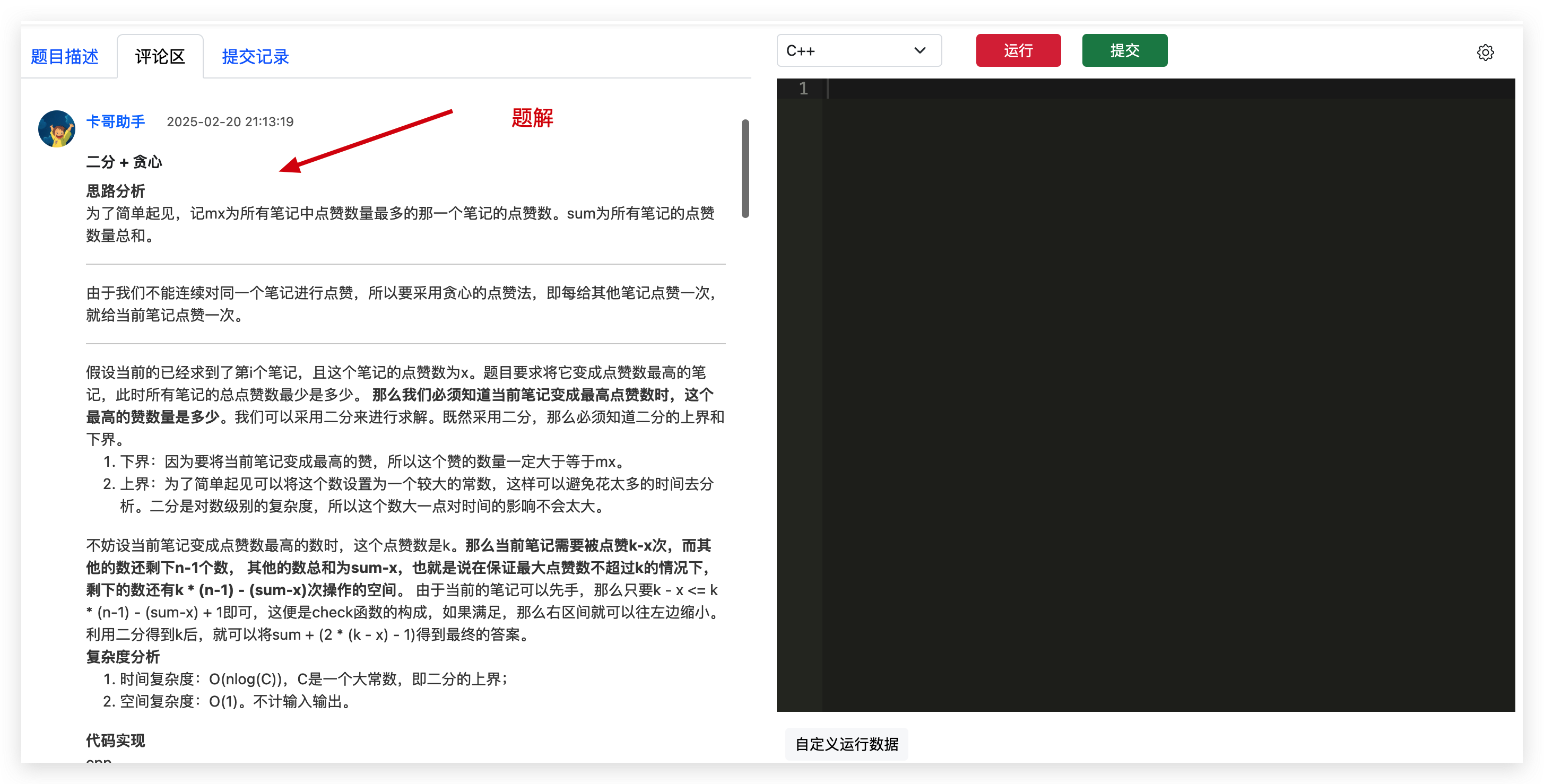
我们的题解,会给出 C++,Java 和 python版本的代码。
原价 199 元,现在预售只需要:46元,随着我们的题库逐步完善,将涨价直到恢复原价。
还可以拼单,如果大家找身边的伙伴拼单购买,40 元就可以拿下!
100 道大厂笔试算法题,附带判题系统 和 题解,合一道题目 3 毛钱。
这个价格还是很接地气的,一赔奶茶,一顿饭钱,就可以刷最近两年的各个大厂笔试题目,有判断系统,有题解,支持各个语言的版本。
大家现在支付后,后面再更新的题目,都可以学习,不用二次付费,所以早加入非常划算。
QA
Q:为什么只有去年的真题,没有今年的真题?
A:大家做去年的真题才有意义,某些厂如果重复出题了,一般都是和去年的题重复,例如 25年秋招,做 24年秋招的笔试真题才有意义,做25年春招题目意义不大。
Q:题目的题解在哪里?
A:在题目评论区,有卡哥助手发的题解。
支付方式
扫码后,会看到,单独购买和拼单购买两种方式, 可以找身边的伙伴拼单,也可以自己和自己拼单。

可以加入拼单群,寻找一起拼单的伙伴:

支付后,大厂笔试题目在卡码网就会自动开动,登录卡码网:https://kamacoder.com/company.php

记得用购买的微信,登录卡码网,就可以看到最近两年的大厂算法题目。
如何使用大厂笔试题库?
1. 完成付款后,您将获得所有大厂笔试真题的访问权限
2. 在"课程内容"选项卡中,您可以按年份和公司查看所有题目
3. 点击题目链接,即可进入题目页面进行练习
4. 在题目页面底部的评论区,您可以找到由卡哥助手提供的详细题解
5. 题解包含多种编程语言(C++、Java、Python、GoLang)的实现
微信扫码购买
